关于轴向流动下细长圆柱束的变形问题研究，主要考虑两个问题：一是，在存在较小变形时，流动的作用是什么；二是，流动和变形之间的耦合关系是怎样的。
通常而言，流动压力载荷对流动的影响，主要取决于流体力和细长结构刚度力的竞争，最终可能导致变形加剧或回到初始状态，如图1所示。这种不稳定性，是在某些条件下，系统在扰动的影响下自发地离开其平衡状态，包括静态不稳定性和动态不稳定性两种类型。
求解这类不稳定性问题的一般方法，通常采用瞬态方法，而这里将采用静态稳定性的直接研究。采用简化的不可压缩、无湍流、无粘度的势流模型来描述流动的不稳定性，并在一个简单案例中通过实验和数值结果进行验证。实验装置的实物图和实验模型示意图如图2和图3所示。
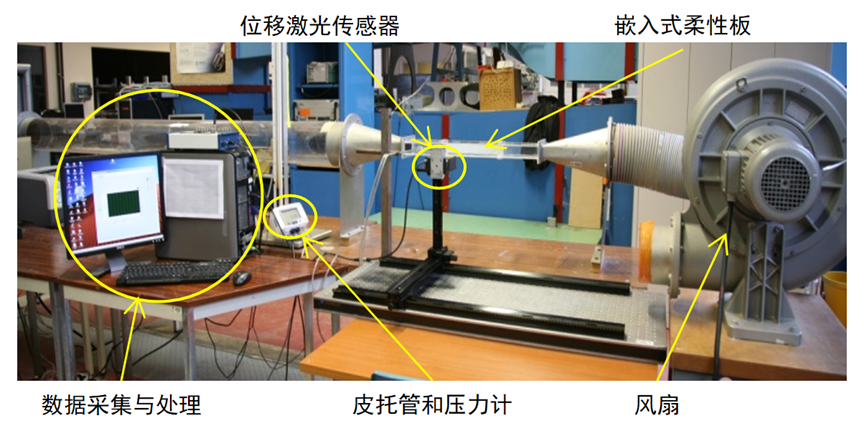
图3 实验模型的示意图
02 解决方案
求解不稳定性问题主要分为两步，第一步如图4所示，循环迭代1到N阶模态，按照各阶模态阵型定义几何模型，生成对应的网格，计算几何模型周围的势流，进而获得流体对板的压力；第二步如图5所示，基于固有模态投影压力载荷，建立静态平衡，寻找系统的特定值，从而确定不稳定性的阈值，即临界失稳速度Ucrit。
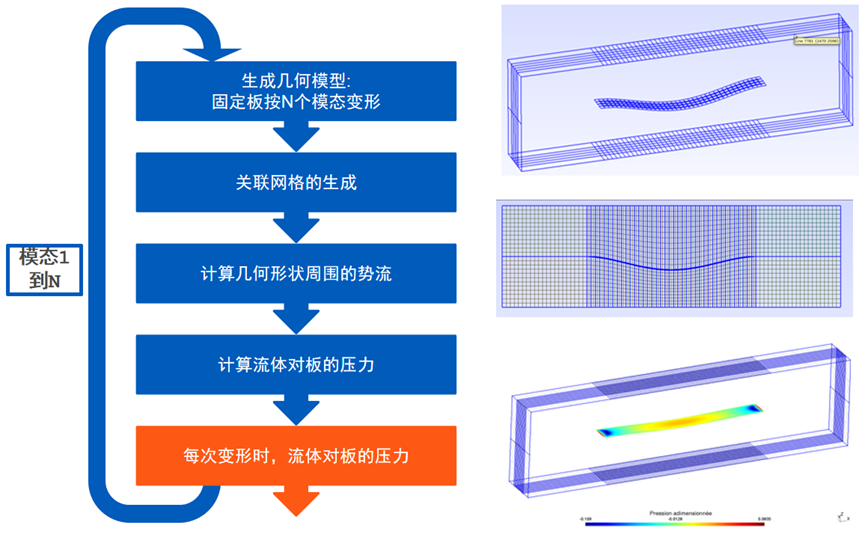
图4 不稳定性问题第一步求解流程
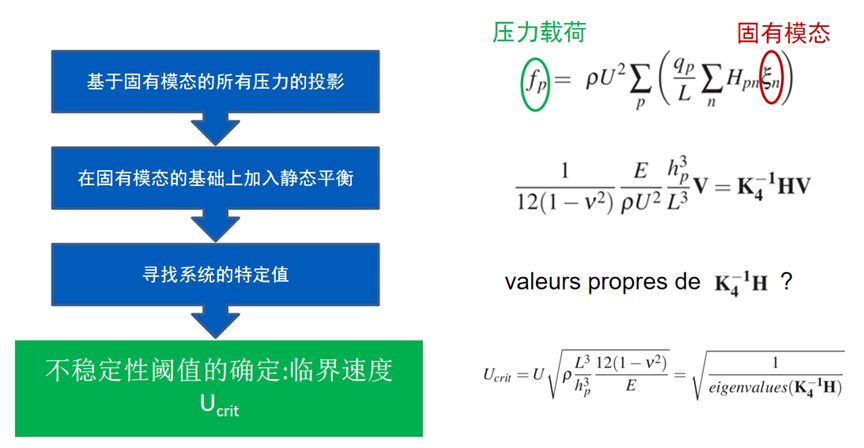
图5不稳定性问题第二步求解流程
本研究中针对拉普拉斯类问题进行有效求解，基于Python内置命令实现自动计算与连续网格，采用固体力学仿真软件求解细长结构在轴向流体作用下的变形问题。
具体而言，先进行流体边界的计算，如图6所示，在一组节点或网格上施加边界条件。采用软件内置的operator THER_LINEAIRE进行势流计算，完成温度场T与势能场φ的转换，将流体速度场等效为流体分量场FLUX，FLUY，FLUZ，再使用operator FORMULE定义压力公式，使用operator CALC_CHAMP计算流场各处的压力，使用operator CREA_CHAMP存储各节点上的压力。该计算模型中的板具有厚度，使得上下边界之间实现物理隔离，允许在板上和板下施加不同的边界条件，并且无需管理流体表面法线，也没有双节点的问题。
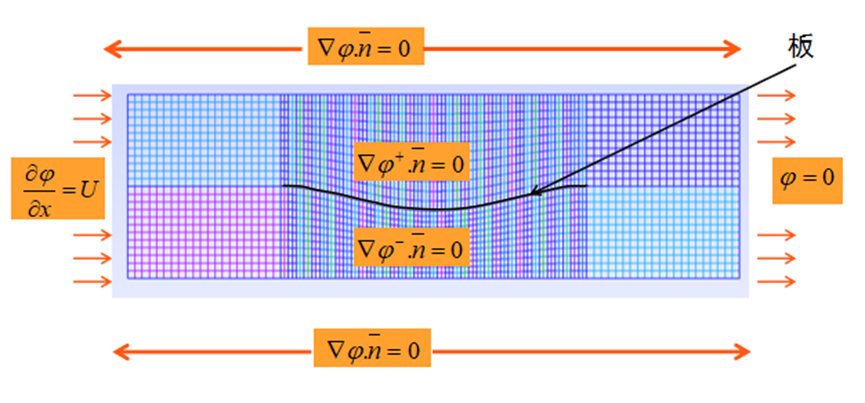图6 流体计算边界条件
基于Python，使用仿真求解器的内置命令按模态循环迭代，在每次迭代中控制几何和物理参数，用命令行生成几何和网格，完成流体荷载的投影和矩阵的生成，确定特征值和计算临界速度。特别地，控制软件在循环的每次迭代中重新读取网格，并且用numpy重新排列软件提供的几何数据以获得剖面上的压力分布。
03 计算结果
图7是实验测得的不同流速下实验件的变形结果，包含两条位移幅值的变化曲线，并且都观察到不稳定阈值的出现，这种不稳定阈值，即临界失稳速度，作为数值方法的验证准则。
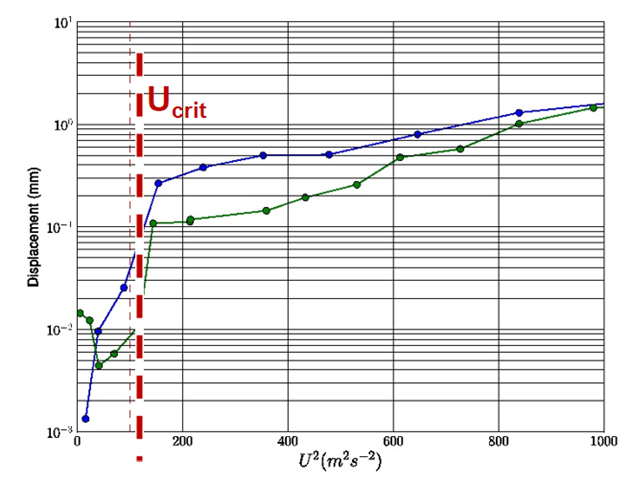
图7 实验测得的位移结果（红线为临界失稳速度）
采用固体力学仿真软件计算模型的网格数量约为35000个，花费30分钟完成10阶模态的30次迭代计算。计算获得基于不同模态的几何模型对应的临界失稳速度，形成数值分析方法的不同初始几何模型的变形与临界速度的关系图，并与实验数据，以及二维静态方法的解析解和二维动态方法的解析解进行比较，如图8所示。可以得出，基于固体力学仿真软件的数值数据与二维静态、动态方法的解析解具有相似的变化趋势，并且更接近于实验测得的数据。
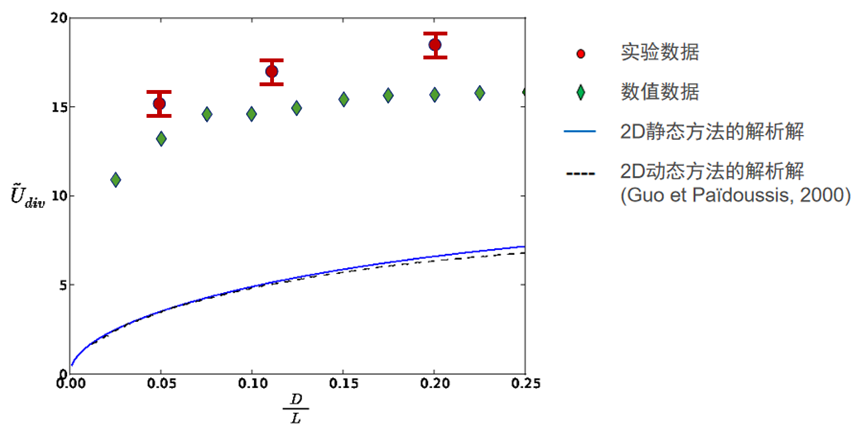
图8 不稳定性问题的临界速度比较
本研究结合Python和固体力学有限元仿真软件进行了轴向流体作用下的细长结构不稳定性的分析，验证了静态直接解法，并进行了参数研究以评估本构模型的影响。后续可以继续在柔性板网络上测试相同的方法，并设置更接近实验状态的边界条件。而更长期的计划，可以预测结构不稳定性之后的行为，并可使用基于固有模态的三维几何模型进行研究。
远算自主研发了短视频水流测速APP，采用先进大尺度粒子图像测速技术，实现快速便捷流速测量的零门槛水利工具，带来“视频一点，流速在手”的超强体验，轻松、便捷地实现河流测速。目前远算还上新了小程序版本，欢迎大家扫码使用！
远算在bilibili、头条、知乎、技术邻定期发布课程视频等内容
敬请关注
2023年5月10日 09:36
