【力学分析】板的弹性屈曲临界应力

在钢结构设计标准中，很多地方都用到了板的弹性屈曲临界应力，比如：截面等级S4限值的计算、S5级截面屈曲后强度计算过程中所用到的均一化长细比λ_np。

因此对板的弹性屈曲分析的了解，可以更好的帮助我们理解规范中宽厚比限值以及屈曲后强度计算。

一、屈曲临界应力-解析解公式

由教材《钢结构稳定理论与设计》第九章“板的屈曲”可得，板的线弹性屈曲临界应力为：

​

其中k为板的屈曲系数，该值与板的长宽比/边界条件/应力类型/应力梯度均有关系。当板受到正应力时为k_σ，受到剪应力时为k_τ

1.1屈曲系数-k_σ

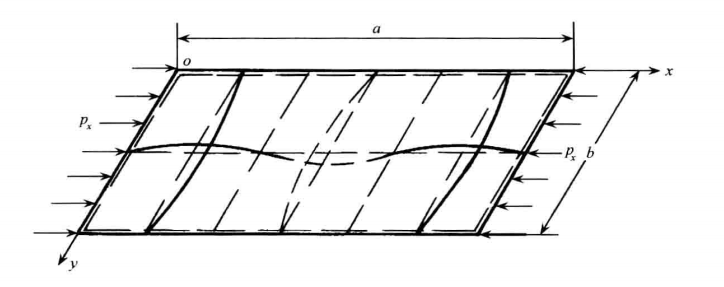
对于狭长形板（a/b>4)，四边简支（不能面外移动，但可面内移动），受正应力，应力梯度为α₀（公式3.5.1）的板，国标GB50017给出的屈曲系数公式为8.4.2-4所示。

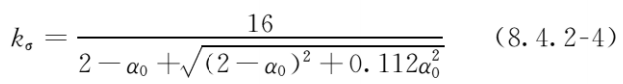
欧标EN1993-1-5表4.1给出的公式是分段式：

​

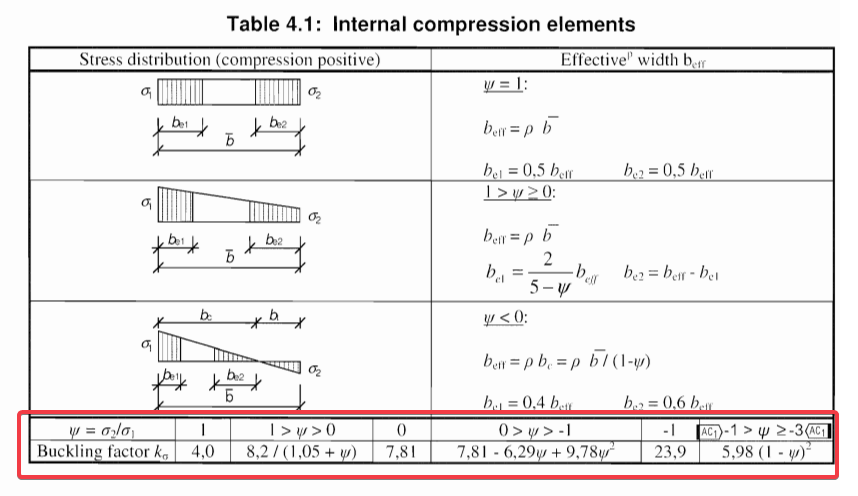
其中的应力比ψ与国标α₀的关系为：α₀=1-ψ

均匀受压时，α₀=0，ψ=1，k_σ=4

纯弯时：α₀=2，ψ=-1，k_σ​=23.9

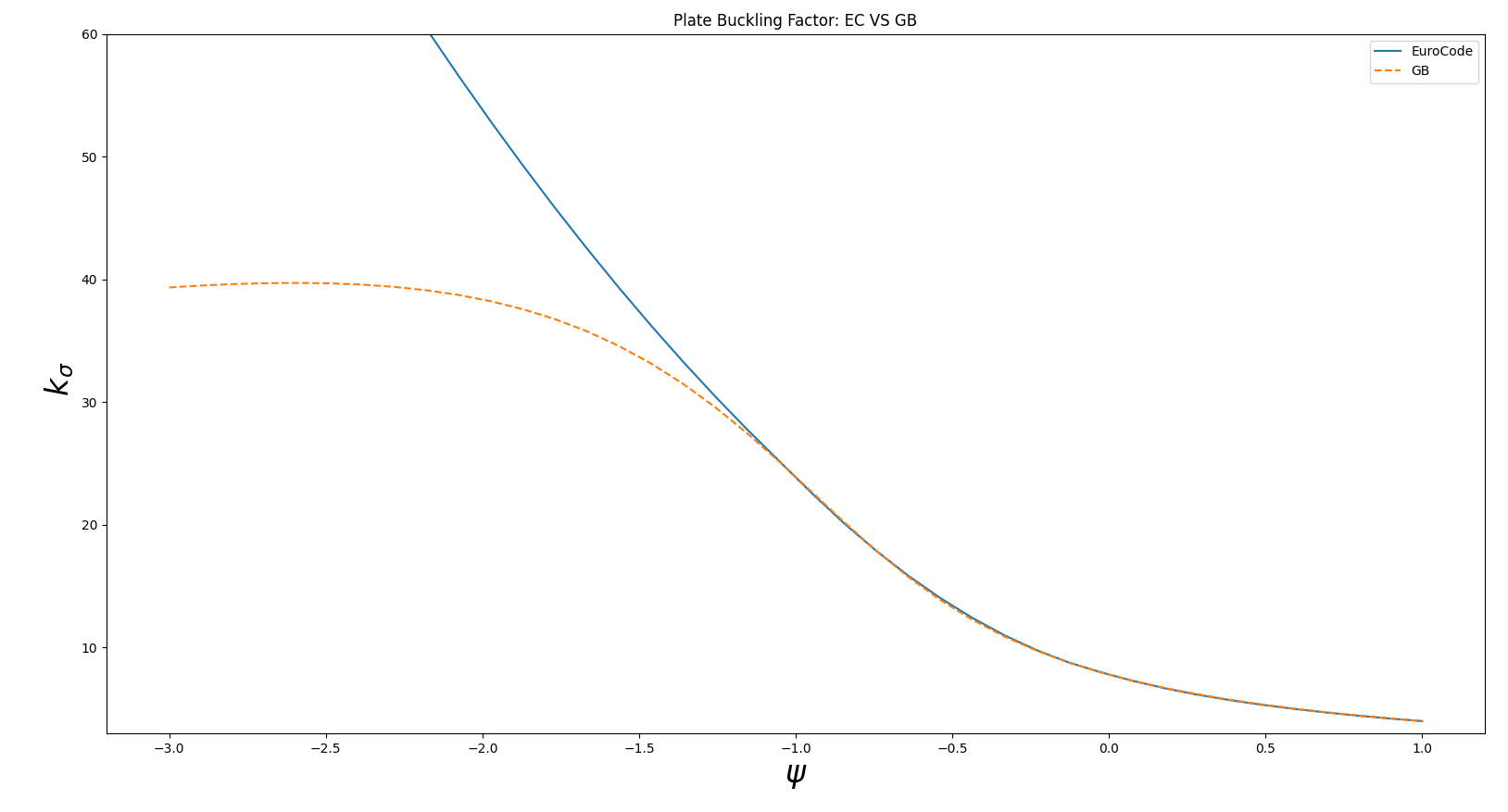
当-1<=ψ<=1时，也就是板的应力状态处于均压、压弯、纯弯时，欧标和国标的屈曲系数是基本一样的。

不同之处在于ψ小于-1时，也就是板件处于拉弯时是有很大差异的。国标的屈曲系数应该只能适用于压弯的情况。

二、压弯屈曲临界应力-解析解VS数值解

这里对比三种情况：

均压ψ=1，k_σ=4

压弯ψ=0，k_σ=7.81

纯弯ψ=-1，k_σ=23.9

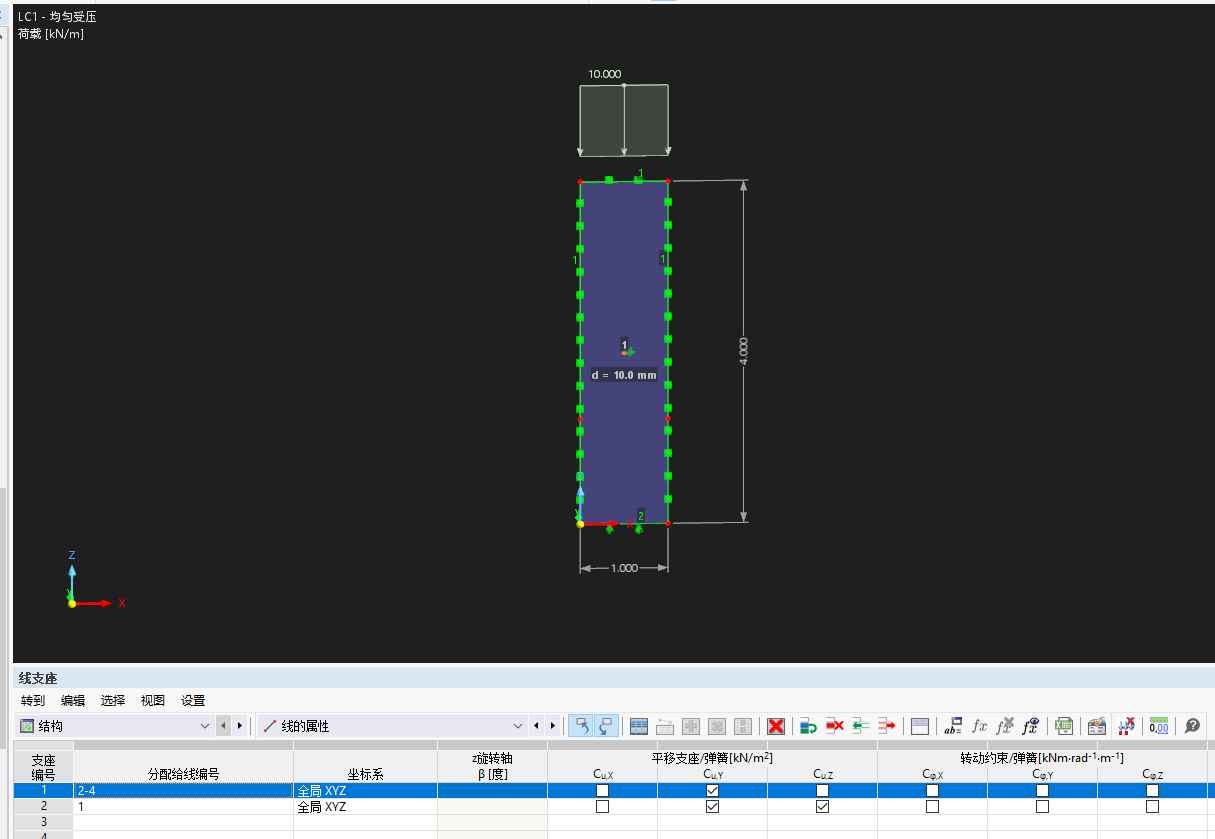
模型参数如上图：

a=4m,b=1m,t=0.01m,Px=10kn/m,σx=Px/t=1Mpa

边界：底部固定Y/Z,其余三边固定Y,面中点固定X

网格尺寸：25mm

2.1解析解

将E=206000Mpa,v=0.3,b=1000mm,t=10mm以及三种情况的屈曲系数（4，7.81，23.9）分别带入前面的解析公式，可以得到三种情况的屈曲临界应力分别为：

均压：74.4Mpa

压弯：145.3Mpa

纯弯：445.3Mpa

2.2数值解

RFEM6中激活“结构稳定分析”并在分析工况中勾选"计算临界荷载"即可。

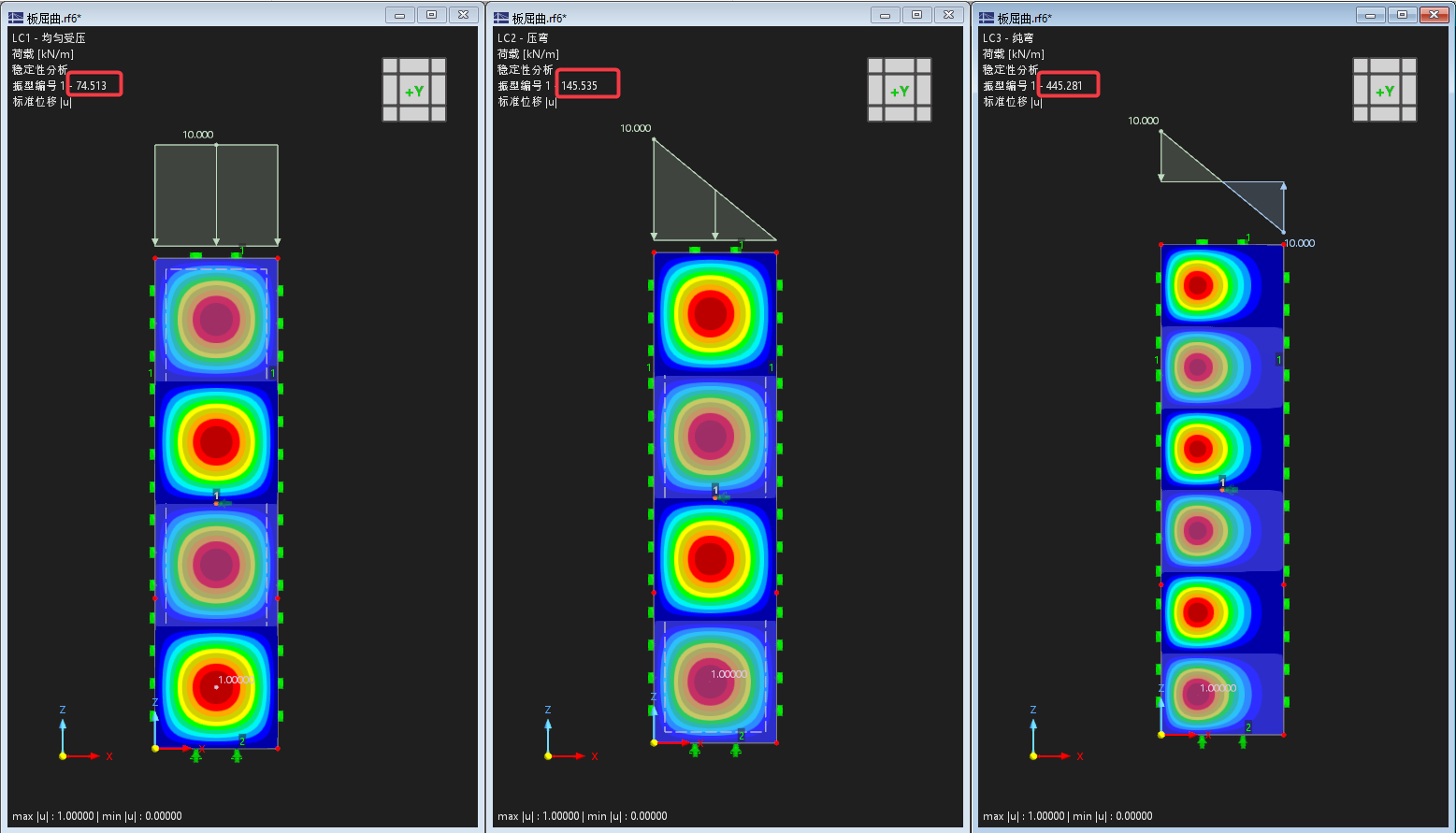
三种情况的数值解分别为：

均压：74.5Mpa，误差0.1%

压弯：145.5Mpa，误差0.1%

纯弯：445.3Mpa，误差0.0%

三、屈曲系数-kτ

当板受剪时，也会产生屈曲，剪切屈曲系数k_τ的计算可由《钢结构稳定理论与设计》9.14a,9.14b得到。

对于四边简支板：

a/b=4时，k_τ=5.59，带入屈曲临界应力公式可得，

解析解：τ_cr=104.35Mpa

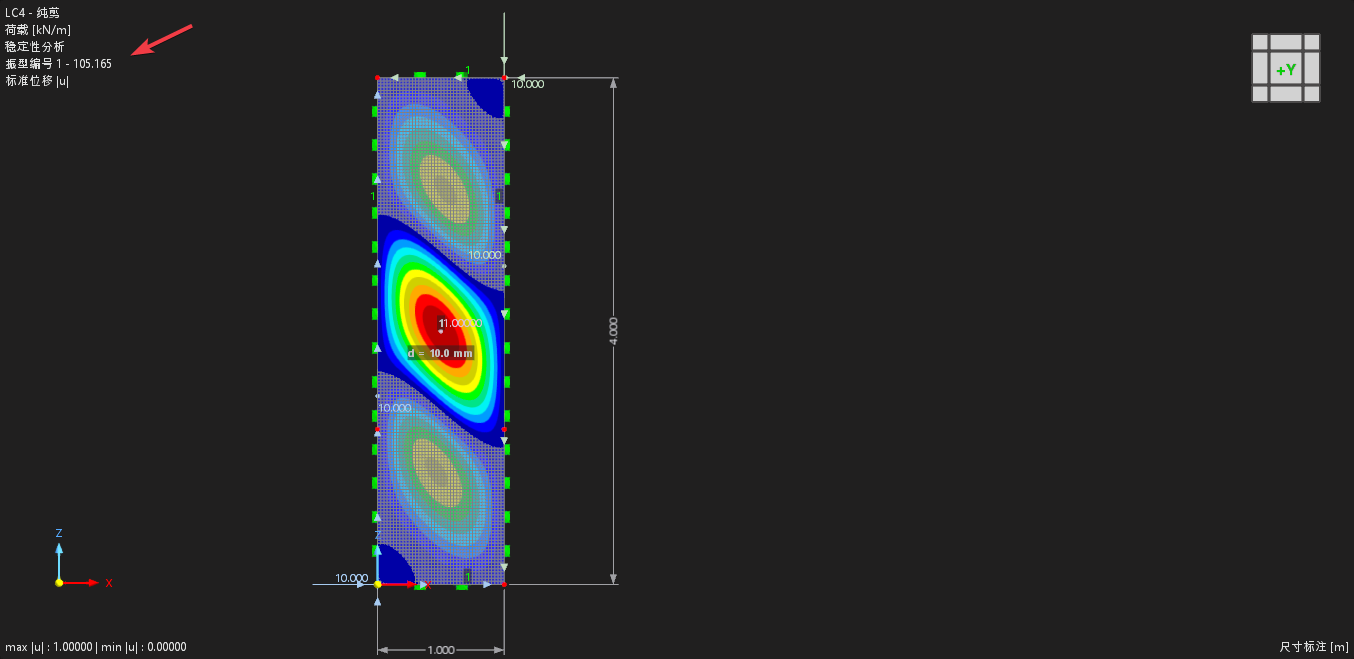
数值解：105.17Mpa,误差0.8%