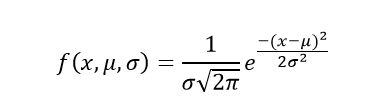Python – 统计中的正态分布

仿真资料吧

2025年2月15日 21:56

概率分布决定了随机变量采用的所有结果的概率。分布可以是连续分布或离散分布，具体取决于随机变量采用的值。概率分布有几种类型，如正态分布、均匀分布、指数分布等。在本文中，我们将了解正态分布，还将了解如何使用 Python 绘制正态分布。

什么是正态分布

正态分布是一个连续概率分布函数，也称为高斯分布，它的平均值是对称的，并且具有钟形曲线。它是最常用的概率分布之一。它有两个参数

Mean（μ） - 它表示分布的中心
Standard Deviation（σ） – 它表示曲线中的分布

正态分布的公式为

正态分布公式

编辑

正态分布公式

正态分布的性质

Symmetric distribution （对称分布） – 正态分布相对于其平均值点是对称的。这意味着分布在其平均值上完全平衡，两侧有一半的数据。
钟形曲线 – 正态分布的图形采用钟形曲线形式，其中大多数点累积在其平均位置。此曲线的形状由分布的平均值和标准差决定
经验法则 – 正态分布曲线遵循经验法则，其中 68% 的数据位于与图表平均值的 1 个标准差范围内，95% 的数据位于与平均值的 2 个标准差之间，99.7% 的数据位于与平均值的 3 个标准差之间。

正态分布中的经验法则

编辑

正态分布中的经验法则

Additive Rule （加法规则） – 两个或多个正态分布之和将始终为正态分布。
中心极限定理 – 它指出，如果我们取从独立和相同的分布式随机变量收集的大型无数据点的平均值，那么这些平均值将遵循正态分布，而不管它们的原始分布如何。

使用 Python 的正态分布

Python 编程语言有几个库，可用于绘制正态分布并获取数据点的概率分布函数。

绘制和应用正态分布所需的模块

Numpy – 一个用于数值数学计算和处理多维 ndarray 的 Python 库，它还具有非常大的数学函数集合来作此数组。
Pandas – 一个基于 NumPy 构建的 Python 库，用于有效的矩阵乘法和数据帧作，它还用于数据清理、数据合并、数据重塑和数据聚合
Matplotlib – 它用于绘制 2D 和 3D 可视化图，它还支持多种输出格式，包括图表
Scipy – 用于求解数学方程式和算法的 Python 库。它是统计和微积分函数最常用的库之一。

我们可以使用这些模块来绘制数据点的正态分布曲线。此外，我们

使用 Python 计算单个数据点的概率分布

import numpy as np

def normal_dist(x, mean, sd):
    prob_density = (np.pi*sd) * np.exp(-0.5*((x-mean)/sd)**2)
    return prob_density

mean = 0
sd = 1
x = 1
result = normal_dist(x, mean, sd)
print(result)

输出：

1.9054722647301798

用于绘制正态分布的 Python 代码

import numpy as np
import matplotlib.pyplot as plt
 
# Mean of the distribution 
Mean = 100

# satndard deviation of the distribution
Standard_deviation  = 5
 
# size
size = 100000
 
# creating a normal distribution data
values = np.random.normal(Mean, Standard_deviation, size)
 
# plotting histograph
plt.hist(values, 100)
# plotting mean line
plt.axvline(values.mean(), color='k', linestyle='dashed', linewidth=2)
plt.show()

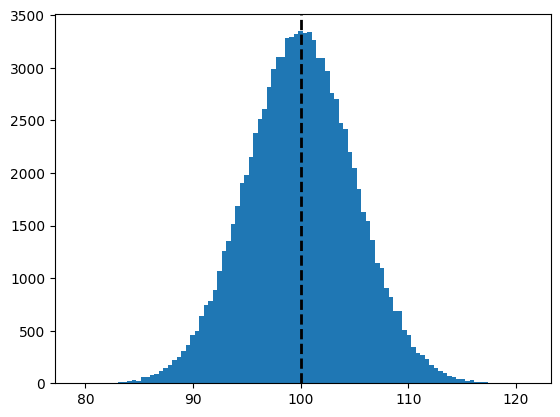
输出：

正态分布图

编辑

正态分布图

Python 的正态分布示例

假设班上有 100 名学生，在其中一项数学测试中，学生在该科目中的平均分数为 78，标准差为 25。学生的分数服从正态概率分布。我们可以使用此信息来回答有关学生成绩的一些问题。

获得低于 60 分的学生百分比的 Python 代码

在这里，我们将使用 scipy.stats 模块中的 norm（）函数，使总体平均值的概率分布等于 78，标准差等于 25。

scipy.stats.norm（） 是一个正常的连续随机变量。它是作为 rv_continuous 类的实例从泛型方法继承的。它使用特定于此特定发行版的详细信息完成方法。

q ： 下尾和上尾概率
x ： 分位数
loc ： 平均值 .默认值 = 0
scale ： [可选]scale 参数。默认 = 1
size ： [tuple of ints， optional] shape or random variates.

结果： 正态连续随机变量

# import required libraries
from scipy.stats import norm
import numpy as np

# Given information
mean = 78
std_dev = 25
total_students = 100
score = 60

# Calculate z-score for 60
z_score = (score - mean) / std_dev

# Calculate the probability of getting a score less than 60
prob = norm.cdf(z_score)

# Calculate the percentage of students who got less than 60 marks
percent = prob * 100

# Print the result
print("Percentage of students who got less than 60 marks:", round(percent, 2), "%")

输出：

Percentage of students who got less than 60 marks: 23.58 %

它指出，大约 23% 的儿童的数学成绩低于 60 分。

分数超过 70 的学生百分比的 Python 代码

获取得分超过 70 的人的百分比。我们首先找到得分低于 70 的人数的概率，然后从 1 中减去概率，得到得分超过 70 的人数。

# import required libraries
from scipy.stats import norm
import numpy as np

# Given information
mean = 78
std_dev = 25
total_students = 100
score = 70

# Calculate z-score for 70
z_score = (score - mean) / std_dev

# Calculate the probability of getting a more than 70
prob = norm.cdf(z_score)

# Calculate the percentage of students who got more than 70 marks
percent = (1-prob) * 100

# Print the result
print("Percentage of students who got more than /
      70 marks: ", round(percent, 2), " %")

输出：

Percentage of students who got more than 70 marks: 62.55 %

分数高于 75 分和低于 85 分的学生百分比的 Python 代码

# import required libraries
from scipy.stats import norm
import numpy as np

# Given information
mean = 78
std_dev = 25
total_students = 100
min_score = 75
max_score = 85

# Calculate z-score for 75
z_min_score = (min_score - mean) / std_dev
# Calculate z-score for 85
z_max_score = (max_score - mean) / std_dev


# Calculate the probability of getting less than 70
min_prob = norm.cdf(z_min_score)

# Calculate the probability of getting less than 85
max_prob = norm.cdf(z_max_score)

percent = (max_prob-min_prob) * 100

# Print the result
print("Percentage of students who got marks between 75 and 85 is", round(percent, 2), "%")

输出：

Percentage of students who got marks between 75 and 85 is 15.8 %

登录后免费查看全文

立即登录

技术邻APP
工程师必备

项目客服
培训客服
平台客服

TOP

Python – 统计中的正态分布

什么是正态分布

正态分布的性质

使用 Python 的正态分布

绘制和应用正态分布所需的模块

用于绘制正态分布的 Python 代码

Python 的正态分布示例

获得低于 60 分的学生百分比的 Python 代码

分数超过 70 的学生百分比的 Python 代码

分数高于 75 分和低于 85 分的学生百分比的 Python 代码

推荐阅读