结构优化设计两大优化算法比较：OC vs MMA

在结构拓扑优化设计技术的发展过程中出现了许多优化算法，其中确定性的算法主要有优化准则法(OC：Optimality Criteria Method)和数学规划法(MP：Mathematical Programming)。这里将从两方面比较OC算法和隶属于MP算法的“移动渐进线方法”(MMA: Method of Moving Asymptotes)。

OC算法从一个空间的一个初始设计点出发，着眼于每次迭代应满足的优化条件，依据迭代公式    来得到一个改进的设计    ，而无需再考虑目标函数和约束条件的信息状态；

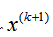
MMA算法，它也从空间的一个初始设计点    出发，沿着某个搜索方向    以适当步长    的迭代格式   ，实现对设计变量的修改，以获得    的值。

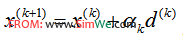
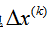
以一个一般的对于多元函数的不等式约束优化问题为例：
 


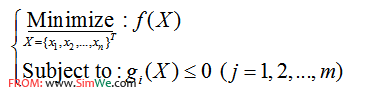
其中，    为设计变量，受到m个不等式约束。

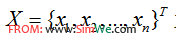
OC算法：
首先构造拉格朗日函数，将有约束的非线性优化问题转化为无约束的优化问题。
其确定最优点主要是根据Kuhn-Tucker条件（驻值条件）
 

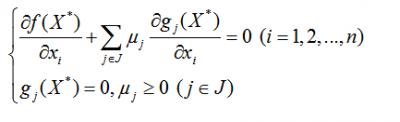
通过引入两个人工参数，阻尼因子    以及移动极限常数    ，使迭代过程稳定。一般采用如下迭代更新形式：

 
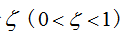
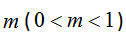
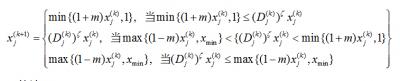
MMA算法：

MMA方法更适于处理目标函数复杂且具有多约束的拓扑优化问题，只要求约束函数对设计变量的微分可以通过解析或者数值方法求得，对复杂的拓扑优化问题，MMA方法具有更好的适定性。MMA方法通过引入移动渐近线，将隐式的优化问题转化成一系列显式的更为简单的严格凸的近似子优化问题，在每一步迭代中，通过求解一个近似的凸的子问题    来获得新的设计变量，而不像OC方法那样直接通过一种显式的启发式的迭代格式来获得新的设计变量。

MMA优化的数学模型表示如下：

 

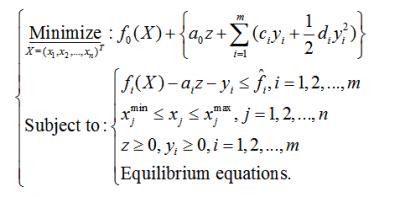
其中：    为给定的大于等于零的常数，    分别是连续可微的函数。
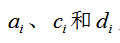
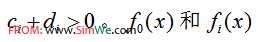
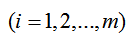
MMA子问题的数学模型为：
 

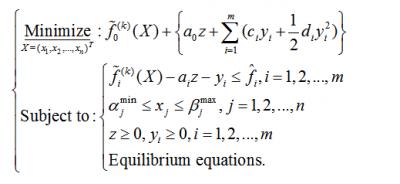
MMA算法还分为GCMMA,GBMMA等类型。有关OC、MMA的详细理论研究可参考华中科技大学罗震博士的毕业论文。

拓扑优化中的源程序
OC算法的源程序实例：

function [xnew]=OC(nelx,nely,x,volfrac,dc)

l1 = 0; l2 = 100000; move = 0.2;

while (l2-l1 > 1e-4)

lmid = 0.5*(l2+l1);

xnew = max(0.001,max(x-move,min(1.,min(x+move,x.*sqrt(-dc./lmid)))));

if sum(sum(xnew)) - volfrac*nelx*nely > 0;

l1 = lmid;

else

l2 = lmid;

end

end

x是原设计变量，xnew为更新后的设计变量。nelx为x轴方向的单元数目，nely为y轴方向的单元数目，volfrac为体积比，dc为敏度分析结果

实例比较：
某悬臂梁的初始边界条件为：
 

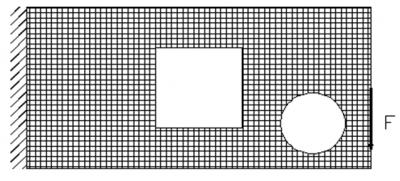
[采用OC算法的最终优化结果（XFEM，红色为子三角形）：
1. 二维图
 
2. 三维水平集函数
 
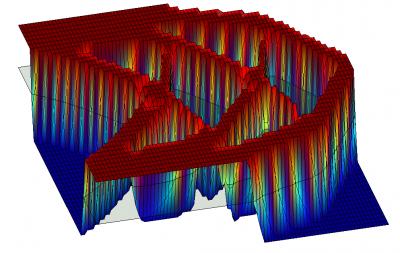
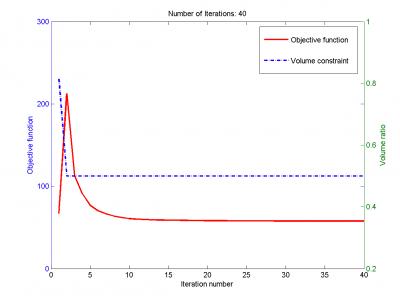
3. 目标函数与体积函数的收敛图
 
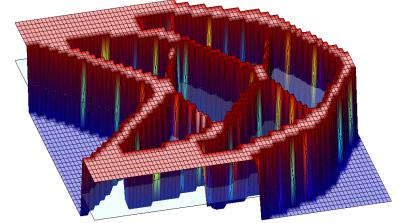
MMA优化结果（常规有限元法，无子三角形）：
1. 二维图
 
2. 三维水平集
 
3. 收敛曲线
 

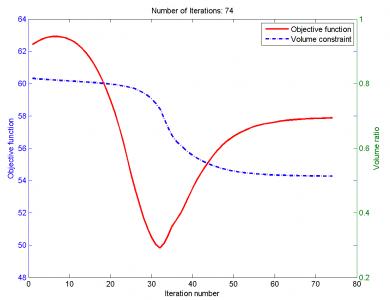
显然OC算法和MMA算法得到了非常相似的优化结果。但收敛过程完全不同。
OC收敛速度很快，10步左右就完成了迭代；MMA则较慢。
对于案例中只有一个约束的优化问题（体积约束50%），OC适应性更好。

----------------------------------------------------------------------------------------

发帖怎么样编辑公式？由于word的公式搬运不上来，只能截图上传，给大家阅读带来了不便~~非常抱歉